문제)
루나와 리나는 타워 건설 게임을 하려고 한다. 타워 건설 게임은 K개의 타워를 사용하는 게임이고 루나는 이 게임을 세팅하려고 한다.
게임 세팅은 서로 다른 높이의 N개의 타워 중 K개를 선택해 원하는 순서로 일렬로 배치하는 것이다. 이때 앞과 뒤에서 바라볼 때 모든 타워가 최소 한 번은 보여야 한다. 즉, 어떤 타워에 대해서 그보다 높은 타워가 그 타워의 앞쪽과 뒤쪽에 모두 존재하면 안된다는 것이다.
게임 세팅을 하던 루나는 문득 게임을 세팅하는 방법이 얼마나 많을 지가 궁금해졌다. 루나를 도와서 게임 세팅을 하는 경우의 수를 구해보자.
입력)
첫째 줄에는 두 양의 정수 N과 K가 주어진다.
둘째 줄에는 각각의 타워의 높이 A1,A2,⋯,AN이 공백으로 구분되어 주어진다.
모든 입력은 정수이다.
출력)
게임 세팅을 할 수 있는 경우의 수를 109+7로 나눈 나머지를 출력한다.
def factorial(n):
result = 1
for i in range(2, n + 1):
result *= i
return result
def nCr(n, r):
f = factorial
return int(f(n) // (f(r) * f(n - r)))
N, K = map(int, input().split())
print((nCr(N, K) * 2 ** (K - 1))%(10**9 + 7))풀이)
우선 식을 정리하기 전에 문제를 다시 한번 정리해보았다.
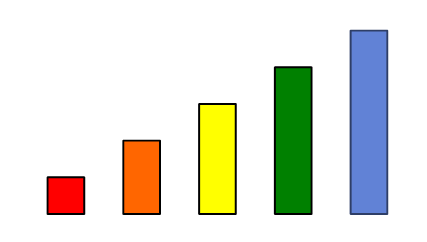
길이가 다른 5개의 타워가 주어졌다. 이 때 3개의 타워 만을 이용한다고 해보자.

타워 3개의 조합은 어떻게든 바뀔 수 있으며, 지금은 예시를 위해 임의로 3개를 선택하였다. 위와 같이 3개를 선택하였을 때, 게임 세팅이 가능한 경우와 불가능한 경우를 알아보자.

위 그림과 같이 타워를 배치할 경우 앞에서 보았을 때, 모든 타워가 한 번에 보이므로 가능한 경우이다.
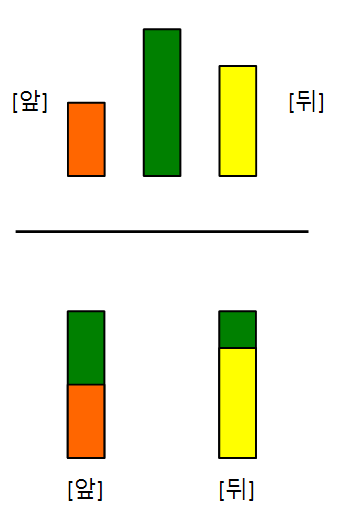
그림 4 같은 경우에도 앞 뒤로 보았을 때, 모든 타워가 한 번씩 보이므로 가능한 경우가 된다.

그림 5의 배치는 가운데 있는 작은 타워가 보이지 않기 때문에 불가능한 경우이다.
위의 그림들로 가능한 경우와 불가능한 경우에 대해 알았다면 이젠 K마다 가능한 경우의 수의 규칙을 찾아보자. 위의 규칙에 따라 K를 2 ~ 4 까지 설정하였을 때, 가능한 경우는 아래의 표와 같다.
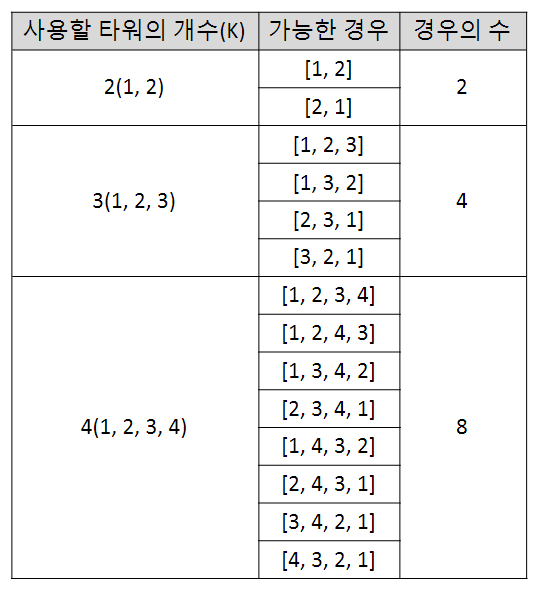
이 때, 경우의 수에 규칙이 있는 것을 확인할 수 있다.
2K-1 = (경우의 수)
해당 수식을 발견하였다면 수식에 따라 코드를 작성하면 된다. N개의 타워 중 K개를 선택하는 식인 조합식 nCr을 정의 해주고(이 때 K가 r의 자리에 들어가게 된다.), K개를 사용할 때 가능한 경우의 수 2 ** (K - 1)을 정의해준다. 그 뒤 출력 조건에 맞추어 109+7로 나눈 나머지를 출력해준다.
ps. nCr의 리턴값을 계산해줄 때, '//'가 아닌 '/'을 사용할 경우 overflow가 발생하게 된다. 자세한 설명은 링크 참조.
'~2025' 카테고리의 다른 글
| 백준) 14888 - 연산자 끼워넣기 [파이썬3] (0) | 2022.07.19 |
|---|---|
| 백준) 15649 - N과 M(1) [파이썬3] (0) | 2022.07.18 |
| 백준) 2981 - 검문 [파이썬3] (0) | 2022.07.15 |
| 백준) 3036 - 링 [파이썬3] (0) | 2022.07.13 |
| 백준) 10814 - 나이순 정렬 [파이썬3] (0) | 2022.07.12 |